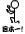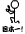ここでは、主に、私が担当している科目
学 部:
物理学スタディー・スキルズ(オムニバス)、物性物理学Ⅰ、物理学特殊講義I、物理学特殊講義II(オムニバス)、物理学総合演習(オムニバス)、物理学実験I、物理学実験III、物理学プロジェクト実験
大学院:
固体電子論I、超伝導特論(電気工学専攻)
に関する補足事項を掲載する予定です。
また、プロフィールや研究内容についても随時掲載していくつもりです。
ここでは、主に、私が担当している科目
学 部:
物理学スタディー・スキルズ(オムニバス)、物性物理学Ⅰ、物理学特殊講義I、物理学特殊講義II(オムニバス)、物理学総合演習(オムニバス)、物理学実験I、物理学実験III、物理学プロジェクト実験
大学院:
固体電子論I、超伝導特論(電気工学専攻)
に関する補足事項を掲載する予定です。
また、プロフィールや研究内容についても随時掲載していくつもりです。

19XX年、東京都品川区に生まれる。
19XX年、東京都立小山台高等学校卒業。
19XX年、早稲田大学卒業、工学博士。
エアロビクス、水泳、お酒(”たしなむ程度”それとも”たしなめられる程
度”?)
| 年 月 日 | 行事内容 | 開催地 | 発表者など | 状況 |
|---|---|---|---|---|
| 平成30年 5月16,16日 | 第34回 希土類討論会 | タワーホール船堀(東京) | 藤澤、高野 | 予定 |
児玉 邦之 鶴林 雅剛 藤澤 孝 森田 雪華子
天球儀の展開図(4.4等星まで示しました。四角が正方形ならば、球面に張り合わすことができます。)


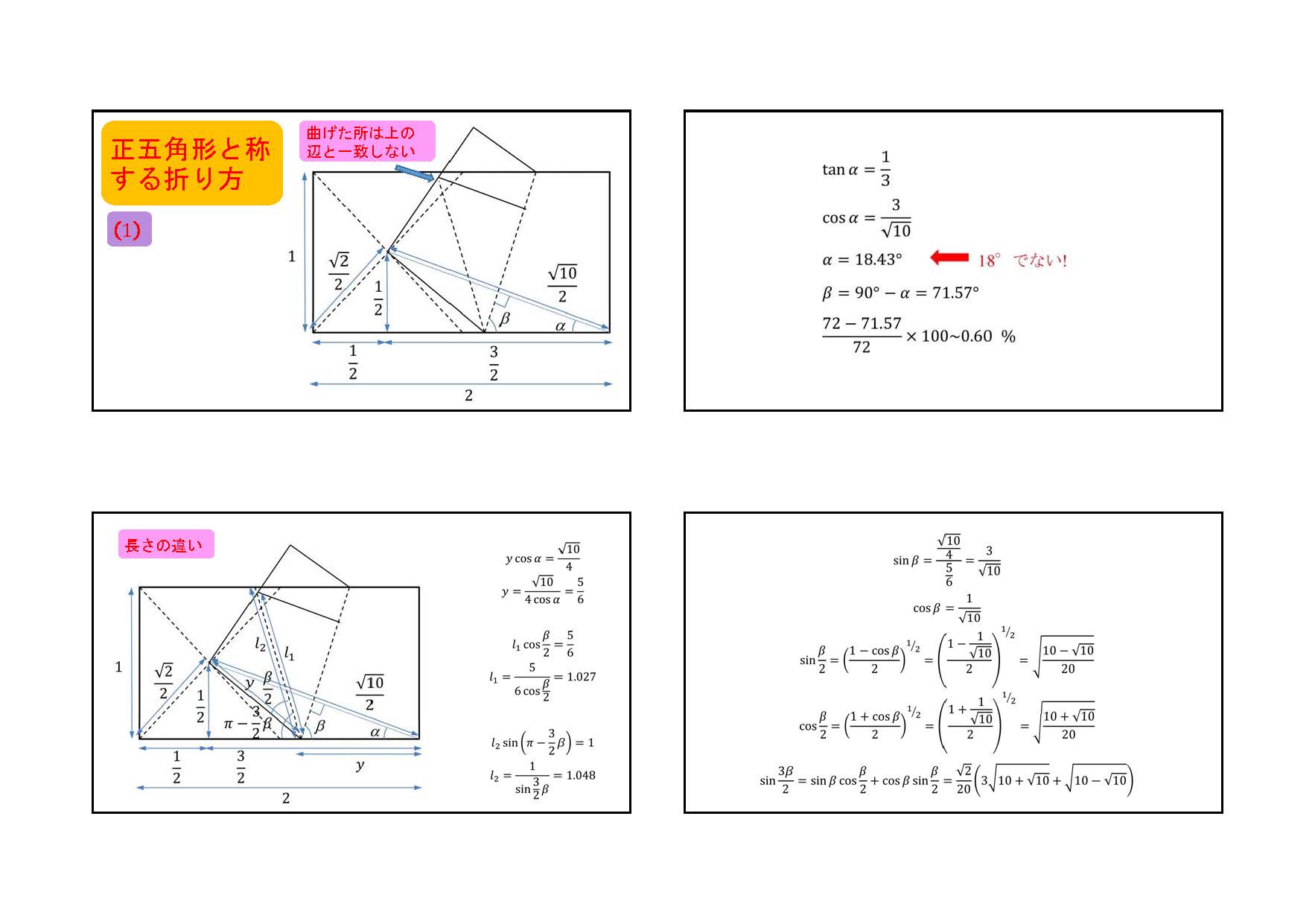
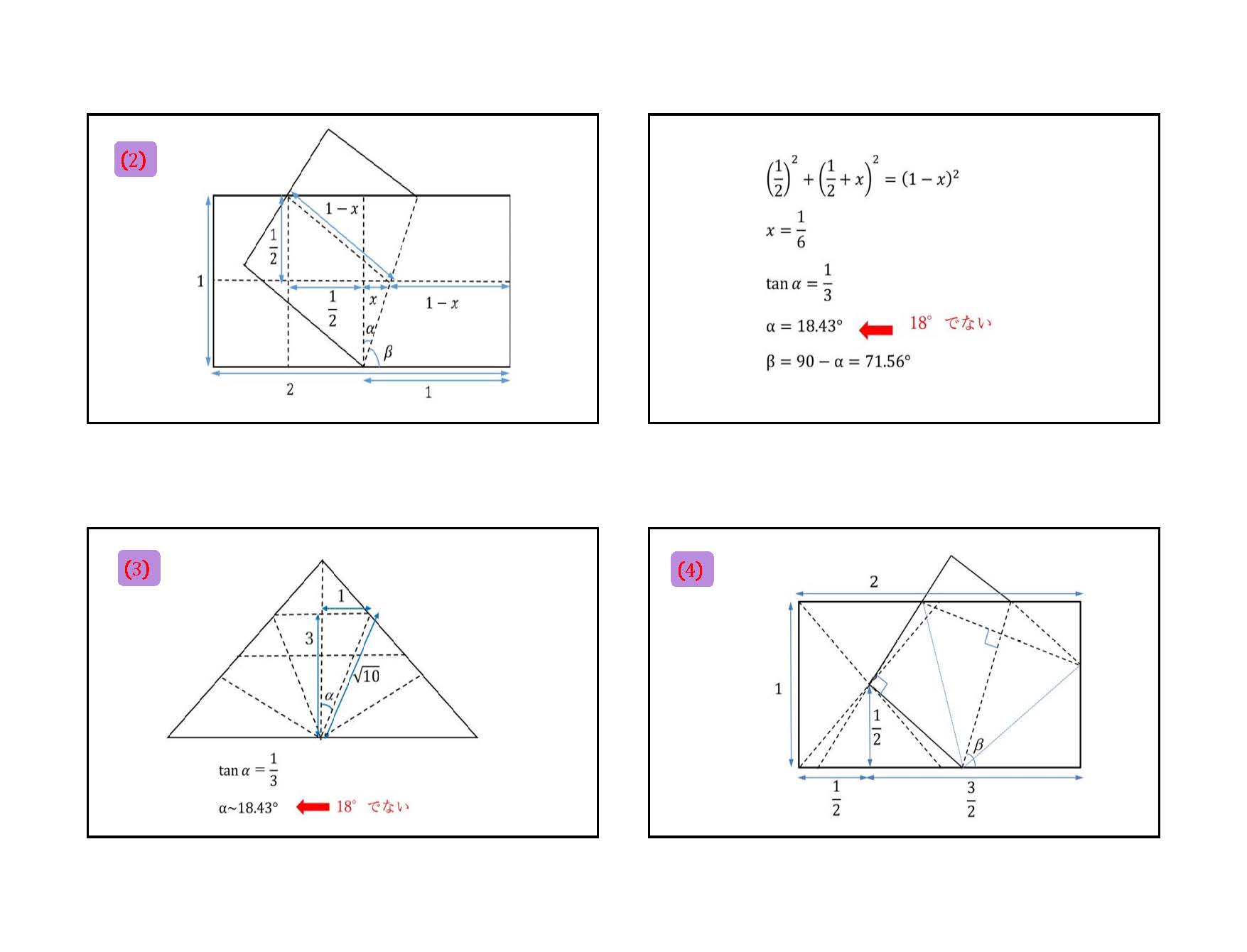
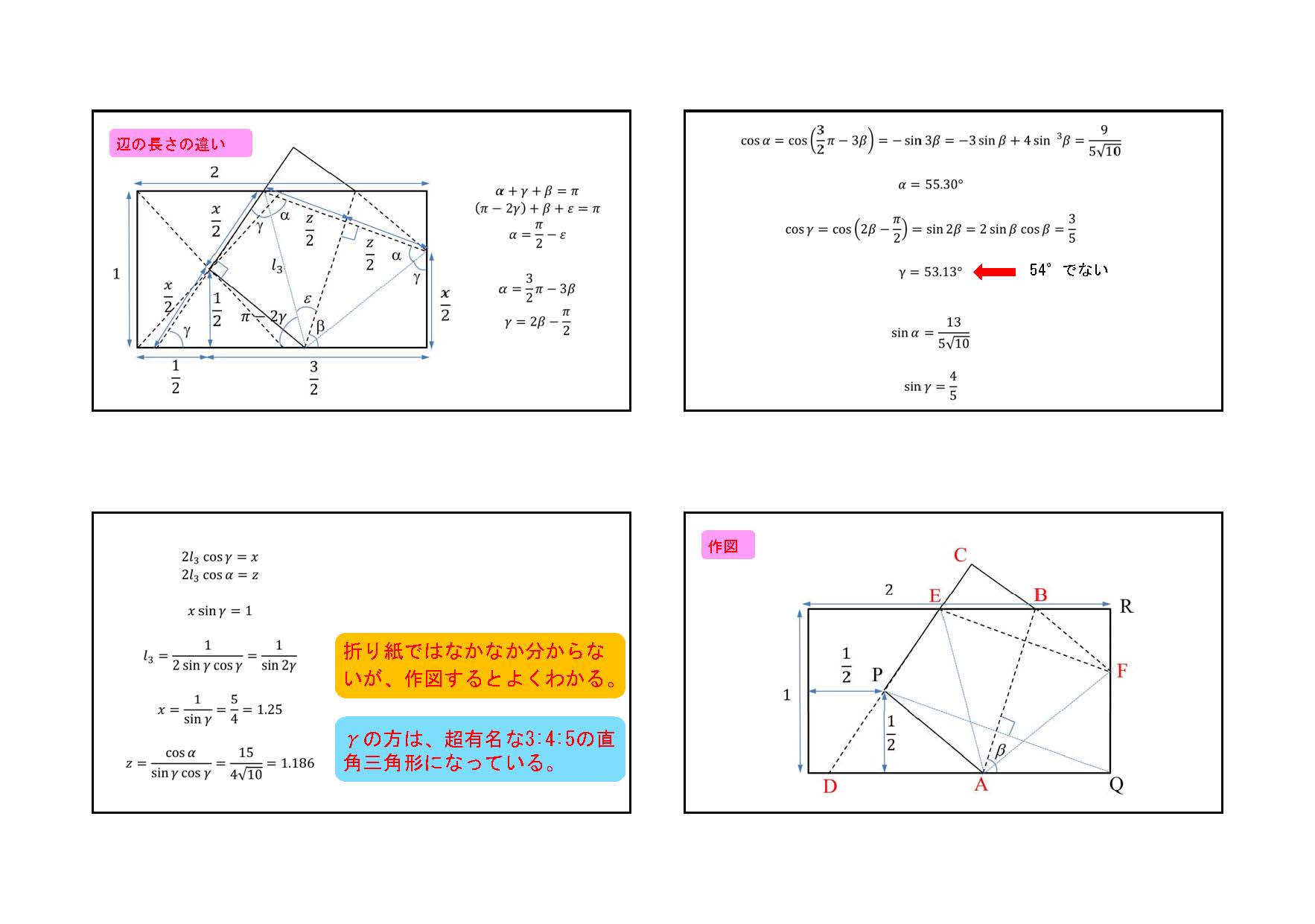
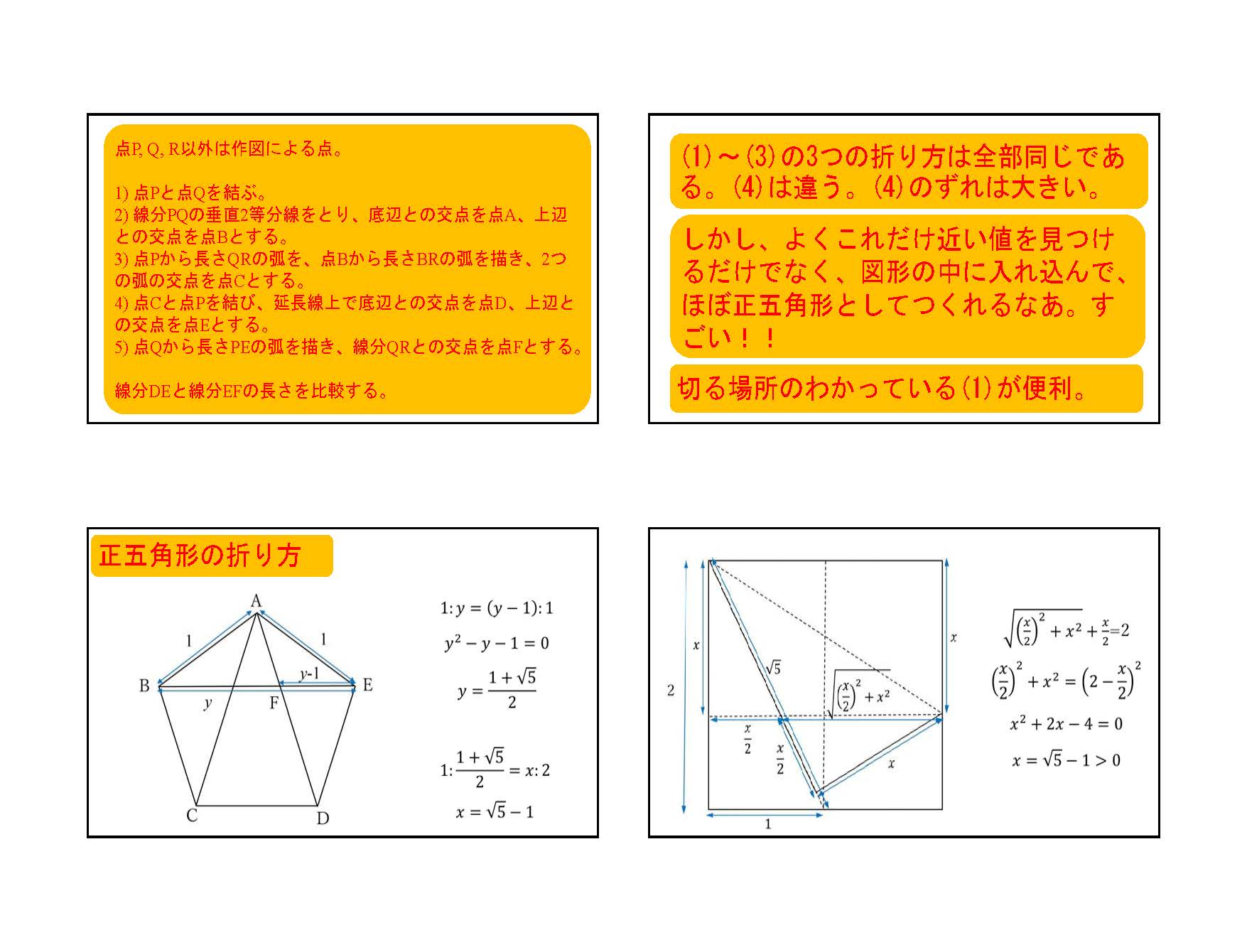
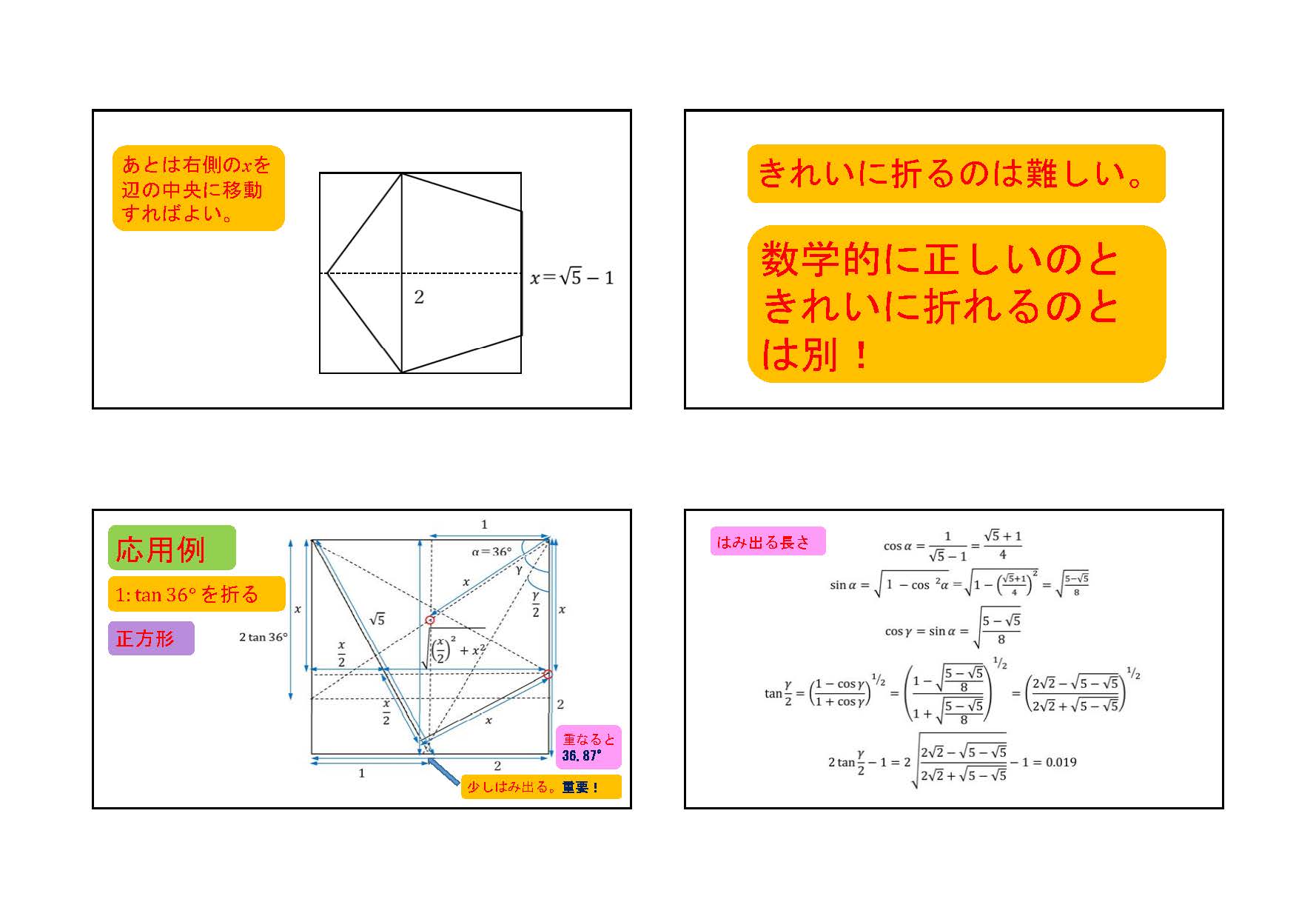
物理学科を希望する高校生の中には宇宙や天文に興味を持っている人たちが多くいます。そのため、オープンキャンパス、出前授業や出前文化祭などでは、上の天球儀作製をよく行っています。しかし、結構かさばるので、場合によっては、星座や星の折り紙をすることがあります。そのときには、正五角形や1 : tan 36°の比の紙が必要になってくるときがあります。そこで、インターネットなどで見られる正五角形の折り方を調べると、疑問に思えることがあったのでまとめてみました。簡単で、本当に正確な正五角形(正しいから正五角形なのだが)の折り方が玉木英彦 著「小学生にピタゴラス」(みすず書房)に載っていました(個人的には昔、玉木英彦 訳「シュポルスキー 原子物理学」にお世話になりました)。その本の中では折り方のみだったので、ここでは、計算して確認しました。他にも正確な正五角形の折り方はあるようです。
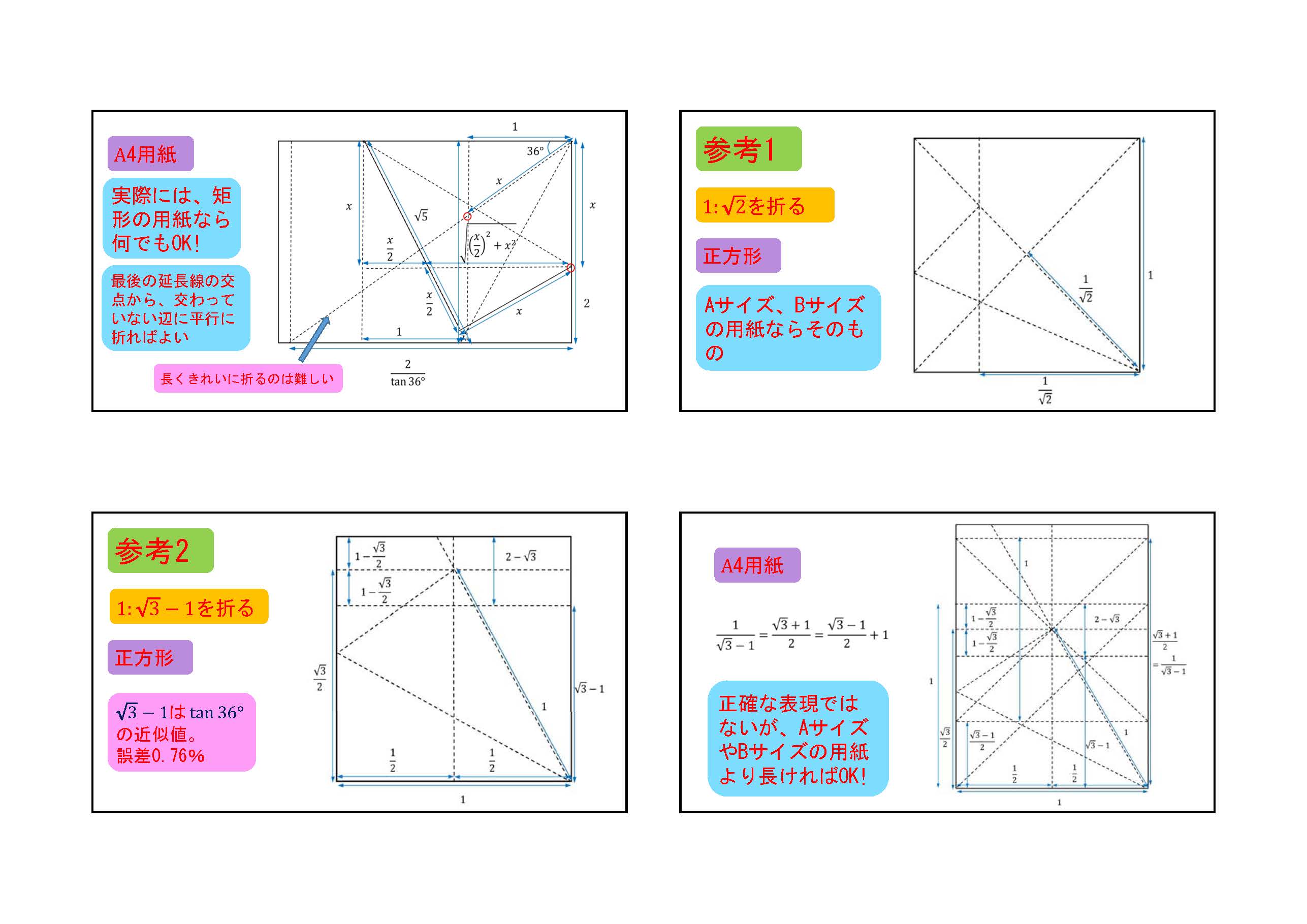
これを応用すると、1 : tan 36°の比の紙も計算したり、測ったりしないで折ることができます。よく、『A4用紙では長い辺を8mmカットする』とありますが、要りません。折り紙に関しては全くの初心者なのでなかなか調べきれないため、すでにどこかに掲載されているかも知れません。また、思い違いや考え違いもあると思いますので、ご意見などをいただければと思います。判断力がまだ十分に備わっていない小学生などに間違った情報を与えたくないので、よろしくお願いします。
使う数学は、三角形の合同・相似、三角比、2次方程式、ピタゴラスの定理、中点連結定理、半角の公式、二倍角の公式、三倍角の公式、加法定理くらいでしょうか。作図も基本的なことだけです。高校生なら確実に理解できます。楽しい練習問題になるでしょうか。三角関数の公式がこんなところで役立つとは思わなかった。数値を求めるときには、多重根号の計算も出てきますが、関数電卓(いまどき使っている人は少ない?)やPCがあれば簡単に求められます。数値が大事なのではなく、解析的に求められることが重要です。数学は大切です。物理にも数学は必須です。
多分、こんな計算は面倒くさくて、やっている人が少ないかもしれませんが、何が正しくて、何が間違っているかを、難しいことは使わないで、基本的なことの積み重ねで、定量的(解析的)に理解することはとても大事です。
また、正方形から1 : tan 36°の比の紙は、折数も少なく、6回折ればできます。どんな矩形(長方形)からでもできるのも汎用性が高いです。用紙を最大限利用しています。
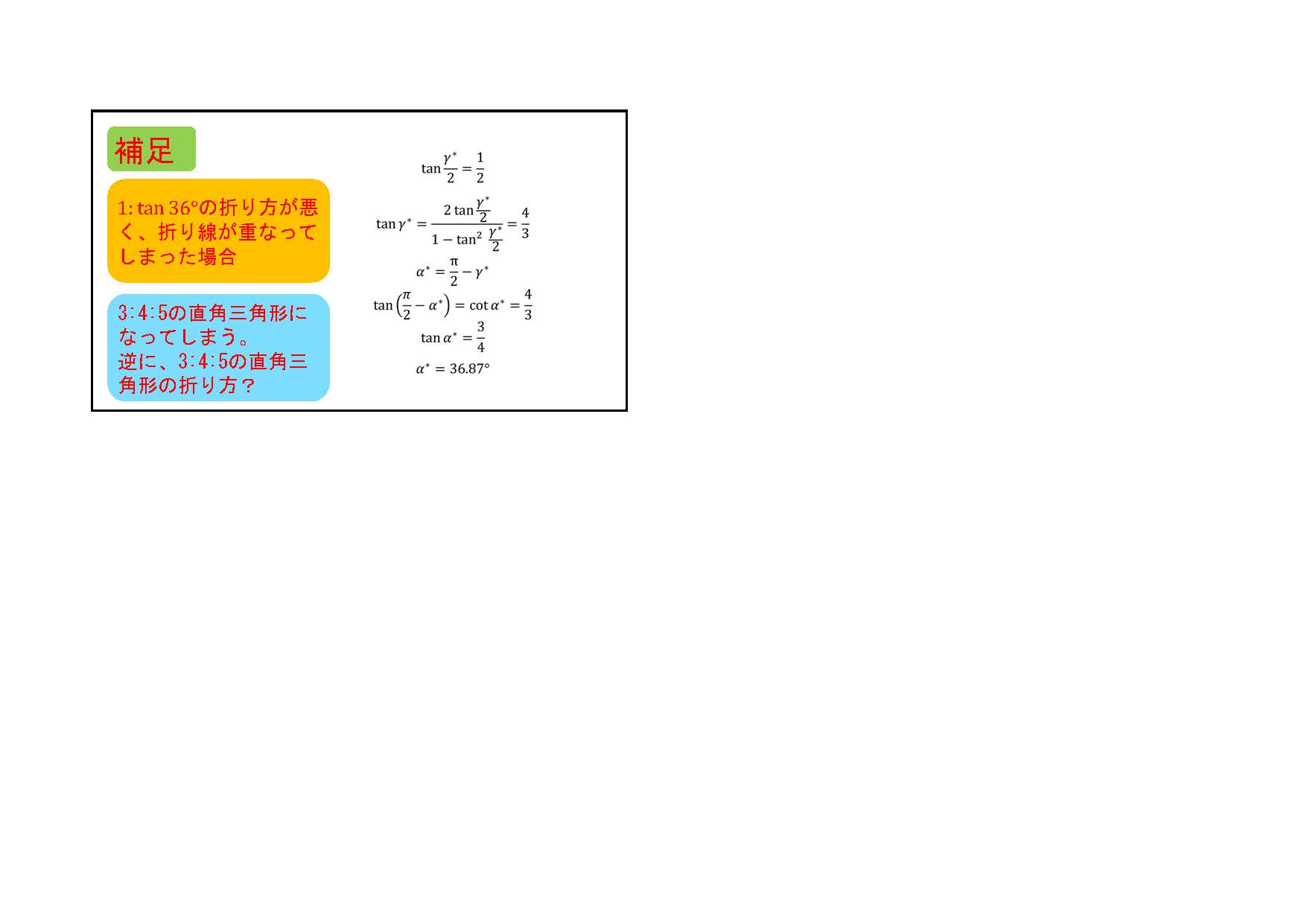
始めに1 : tan36°を折りたいという気持ちがありましたが、どうしていいかわからなかったところ、tan36°と√3-1が非常に近いことをある方のHP(「晴耕雨折 ‐折り紙な日々‐」2015年12月16日)で知り、正三角形の折り方を調べていたら、√3-1の折り方が分かりました。中点連結定理を使います。これは正方形だからできた結果です。正方形からは5回折ればできます。A4用紙での1: √3-1の拡張も、分母の有理化をしているときに分かりました。辺の長い方を有効に使えます。これで満足していたのですが、どうしても1 : tan36°を折りたい、正五角形にヒントがあるに違いないと思い、正五角形の折り方を調べていたところ、玉木英彦氏の著作にあたりました。その折り方では、√5-1が正方形の頂点のところにあったので、すぐに思いつきました。
物事は思い、願い続ければ必ず叶うといろいろな人が言っていて、そんなのはまやかしだと思っていましたが、これについては本当だと思いました。
資料については、2次使用は歓迎ですが、出典を明らかにしていただければと思います。